L`Électronique Numérique

Aujourd`hui l`électronique numérique est de plus en plus présente dans l`équipement de tout les jours. Les objets possédant un système numérique peuvent aller de l`ordinateur au mixeur en passant par les systèmes embarqués dans le monde de l`automobile. Un système numérique permet d`exécuter des taches complexes avec un circuit de petite taille. De plus en plus l`électronique traditionnelle laisse la place à l`électronique numérique. Cette progression est très visible dans le domaine de l`audiovisuelle, avec l`apparition des téléviseurs numériques.
Nous allons voir les bases de cette électronique qui est à l`ordre du jour...

Le Numérique :

Un système est dit numérique lorsqu`il est capable le traiter des valeurs numériques. Ces valeurs sont traités de façon binaire dans le circuit. Il y a seulement 2 états différents possibles en binaire : `1` et `0`. Les transferts de données entre les différents composants du système s`effectuent donc a l`aide de '1' et de '0'. Il existe plusieurs standards pour les niveaux électriques numériques (Ex: TTL, CMOS).

Comme vous pouvez le voir, en mode TTL (c`est le standard le plus utilisé en informatique) le niveau '1' est désigné par une tension de 5 Volts et le niveau '0' est désigné par une tension de 0 Volts.

Si vous voulez interfacer un composant CMOS avec un autre composant de type TTL , n'oubliez pas de d'utiliser des composant pour adapter les niveaux.

En effet, comme vous pouvez le voir ci-dessus, en TTL le seuil du passage à l'état 1 est plus bas que celui du CMOS. Donc certains composants TTL ne délivrent pas une tension suffisante pour contrôler un composant CMOS (le niveau 1 du TTL -> CMOS peut se retrouver dans la zone d'incertitude). Vous pouvez alors avoir des problèmes de fiabilité. Dans le cas d'une alimentation en 5V vous pouvez utiliser des 74HCT244 pour adapter les 2 technologies entre elles. (La série HCT est compatible CMOS et TTL).
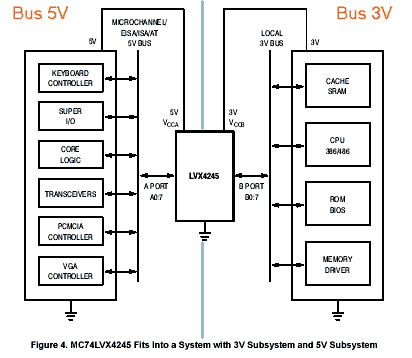
Si vous travaillez sur un système ayant plusieurs bus de niveaux logique différents, il faut bien sur utiliser un composant spécialisé pour les interfacer ensembles. Pour adapter un bus 3.3V avec un bus 5V vous pouvez utiliser un transceiver du type 74LVX4245.
Ci-dessous un exemple concret d'utilisation de l'adaptation de niveau : Adaptation entre le Bus processeur (3V) et les Bus d'extensions (ISA,...) dans un PC.

Les Fonctions Logiques:

Les fonctions de bases de l`électronique numérique sont les fameuses fonctions ET, OU, OU EXCLUSIF, etc.
Voici les tables de vérités de ces fonctions ainsi que leurs représentations schématiques.

La fonction NON (NOT):

E1 S 0 1 1 0

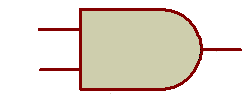
Les fonctions ET (AND) et NON ET (NAND)

E1 E2 S 0 0 0 0 1 0 1 0 0 1 1 1	E1 E2 S 0 0 1 0 1 1 1 0 1 1 1 0

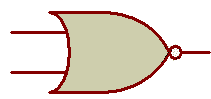
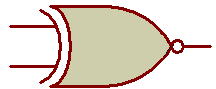
Les fonctions OU (OR), NON OU (NOR), OU EXCLUSIF (EXOR), NON OU EXCLUSIF (EXNOR):

E1 E2 S 0 0 0 0 1 1 1 0 1 1 1 1	E1 E2 S 0 0 1 0 1 0 1 0 0 1 1 0	E1 E2 S 0 0 0 0 1 1 1 0 1 1 1 0	E1 E2 S 0 0 1 0 1 0 1 0 0 1 1 1

Les 2 premières colonnes des tableaux représentent l'état des 2 entrées de la fonction. La dernière colonne représente la sortie de la fonction.
Chaque ligne représente un état indépendant par rapport aux autres lignes.

Ces fonctions sont présentes dans de nombreux composants. Les plus connus de ces composants font partie de la série 74XX (famille TTL).
Voici les principaux composants de la série 74XX (Cliquez pour agrandir):

 

Pour pouvoir réaliser ses circuits il faut savoir comment la ou les sorties doivent se comporter suivant l'état des entrées. Pour cela on fait une mise en équation du circuit. On utilise pour cela l'algèbre de Boole. L'algèbre de boole permet de gérer des variables pouvant avoir 2 états différents (0 ou 1), avec 3 fonctions principales : OU (notée +), ET (notée . ), NOT (notée / ).

Voici une fonction à 4 entrées en exemple: f(a,b,c,d) = a + /((b+/c).a) +/d.(/b + c) -> a OU NOT((b OU NOT c) ET a) OU (NOT d ET(NOT b OU c)

voici la liste des lois de l'algèbre de Boole :

Commutativité :

x + y = y + x
x . y = y . x

Associativité :

x + ( y + z ) = ( x + y ) + z
x . ( y . z ) = ( x . y ) .z

Elément neutre :

x + 0 = x
x . 1 = x

Eléments absorbants et symétriques:

x + 1 = 1
x . 0 = 0

x + /x = 1
x . /x = 0

Invariance:

x + x = x
x . x = x

Distribution :

x . ( y + z ) = x . y + x . z
x + ( y . z ) = ( x + y ) . ( x + z )

Lois de Morgan :

/( x . y ) = /x + /y
/( x + y ) = /x . /y

Toutes ces lois vont permettre de simplifier les circuits logiques efficacement.

Voyons un exemple pour mieux comprendre :

Nous voulons créer un circuit à 4 entrées (a,b,c,d) et 1 sortie (s) qui à comme table de vérités (table qui décrit l'état des sorties suivant les entrées) ceci :

a	b	c	d	s
0	0	0	0	0
0	0	0	1	0
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

 

si on prend les cas le circuit dit '1' le système s'écrit :

s = ( /a . /b . c . /d) + ( /a . b . c . d) + ( a . /b . /c .d ) + ( a . b . /c . d )

si on câble ce circuit directement il nous faudra 22 portes (donc 6 composants environ...)

factorisation :

s = /a .(( /b . c . /d) + ( b . c . d)) + a.d ( /b . /c + b . /c )
s = /a .c.(/b./d + b .d)) + a.d ( /b . /c + b . /c )

simplification second membre (b inutile):

s = /a .c.(/b./d + b .d)) + a.d /c
(/b./d + b .d) est la fonction XNOR de b et d

donc

s = /a.c.(b xnor d) + a./c.d

on a donc finalement 8 portes logiques .....

en câblant le circuit on a:

 

 

Autre méthode: le tableau de Karnaugh

Le tableau de Karnaugh est une méthode qui va permettre d'effectuer des simplifications beaucoup plus rapidement sans avoir à écrire de longues équations.

 

cd\ab	00	01	11	10
00	0	0	0	0
01	0	0	1	1
11	0	1	0	0
10	1	0	0	0

 

Grâce au tableau on peut écrire l'équation s = /a./b.c./d + /a./b.c.d + /c.d.a = a./c.d + /a .c.(/b./d + b . d)

 

Logique sequentielle

 

La Bascule RS :

Symbole :	Table de Verité
	S R Q /Q Etat 0 0 Qn-1 /Qn-1 Pas de changement 0 1 0 1 Reset 1 0 1 0 Set 1 1 ? ? Indeterminé

Schéma interne d'une bascule RS :

un exemple de chronographe de la bascule RS :

La bascule RS avec horloge :

 

Symbole :	Table de Verité
	S R Q /Q H Etat 0 0 Qn-1 /Qn-1 Front montant Pas de changement 0 1 0 1 Front montant Reset 1 0 1 0 Front montant Set 1 1 ? ? Front montant Indeterminé

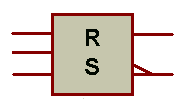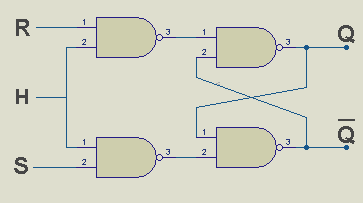
Schéma interne d'une bascule RSH :

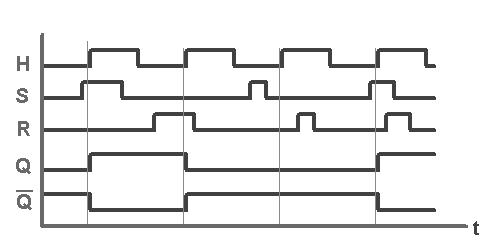
un exemple de chronographe de la bascule RSH :

La bascule Maitre Esclave RS avec horloge :

Schéma interne:

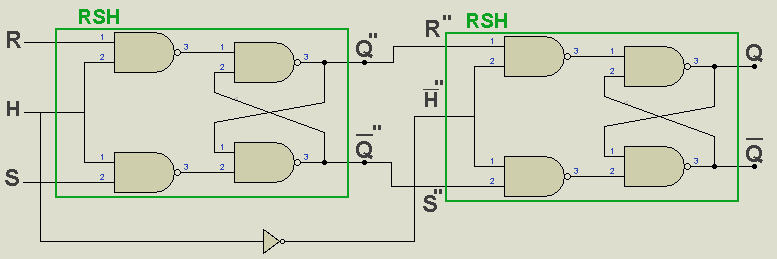
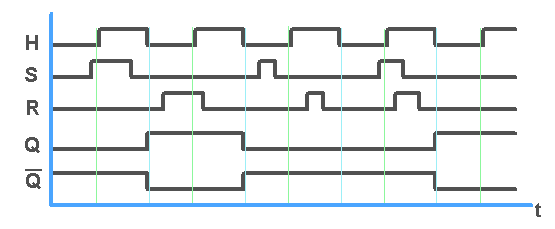
un exemple de chronographe de la bascule M/S RSH :

La Bascule T (Toggle):

Schéma interne:

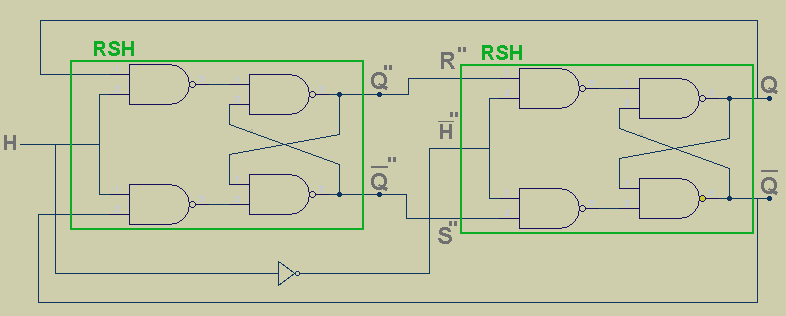
un exemple de chronographe de la bascule T:

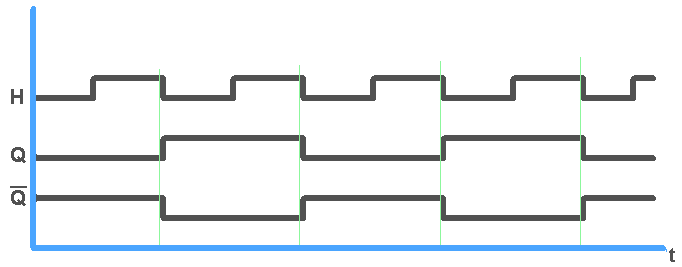
-> Diviseur de fréquence par 2

La Bascule D:

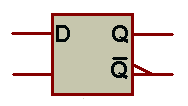
Schéma interne:

un exemple de chronographe de la bascule D:

-> Memoire

La Bascule JK avec Horloge ,Preset et Clear:

Symbole :	Table de Verité
	J K Q /Q /PS /C H Etat 0 0 = = 1 1 Front montant Pas de changement 0 1 0 1 1 1 Front montant Reset 1 0 1 0 1 1 Front montant Set 1 1 /Qn //Qn 1 1 Front montant Toggle ~ ~ 1 0 0 1 ~ Etat Set forcé ~ ~ 0 1 1 0 ~ Etat Reset forcé ~ ~ ? ? 0 0 ~ Indeterminé

un exemple de chronographe de la bascule JK:

Les compteurs :

Compteurs Asynchrones:

Compteur Synchrone:

Compteur de johnson :

Compteur Ring:

La Suite très prochainement...